La plupart des mesures que l'on obtient des expériences en biologie suivent approximativement une distribution dite "normale", ou "gaussienne", dont la densité a la forme d'une cloche, symétrique avec un unique sommet au milieu. C'est aussi l'hypothèse d'un grand nombre d'outils d'analyse statistique. Mais que faire quand on observe deux sommets ou plus ? Le plus probable, c'est qu'on observe alors un mélange de plusieurs composantes normales, qu'on voudrait séparer. Une fois décomposées, on peut travailler sur chaque composante séparément. Le tout s'appelle un "modèle de mélange gaussien", ou "gaussian mixture model" en anglais pour la littérature.
Les exemples d'utilisation sont fréquents. D'ailleurs, si j'ai choisi d'écrire sur ce sujet, c'est que j'ai reçu il y a quelques jours le message suivant :
Salut,
J'ai un service à te demander! J'ai une série de 100 points qui représentent des distances d'expression de gène entre deux cellules après division. J'obtiens une distribution qui n'est pas une gaussienne, et j'aimerais savoir s'il y a moyen de trouver une double gaussienne qui pourrait modéliser de façon adéquate ma distribution. Le but étant de fixer un seuil pour les paires de cellules avec une distance élevée. Est-ce que tu pourrais me montrer comment faire ça? C'est assez urgent…
A.
Pour déterminer quel individu appartient à quelle composante, la méthode usuelle est d'utiliser un algorithme EM (pour Expectation-Maximization). Le résultat de l'algorithme est un ensemble de paires (moyenne, variance) - une pour chaque composante normale - , et une probabilité "a posteriori" pour chaque observation d'appartenir à telle ou telle composante.
Sans entrer dans les détails, l'algorithme fonctionne en alternant deux phases : on attribue - arbitrairement, la première fois - chaque point à l'une des composantes (phase E), dont on peut alors estimer la densité de probabilité (phase M). Puis on considère fixes les densités, et on redistribue au mieux les points entre elles (phase E), par un critère de maximum de vraisemblance. Et on recommence : on recalcule les densités (phase M), etc. On peut montrer que chaque itération améliore la vraisemblance, et donc qu'on converge toujours vers un maximum local.
On peut voir la méthode comme une forme d'apprentissage non-supervisé (clustering).
En pratique
Voici comment faire en utilisant le langage R. Pour ne pas s'encombrer avec l'import de données réelles, générons des données aléatoires, à partir de deux distributions normales, mélangées dans un même vecteur :
# Deux populations normales mélangées: # 1000 points de N(2,1) et 400 points de N(6,1.5). set.seed(100) data = sample(c(rnorm(1000,mean=2,sd=1),rnorm(400,mean=6,sd=1.5)))
C'est-à-dire, ça :
Mais comme les points sont difficilement visibles, on préfère en principe dessiner un histogramme ou une courbe de densité, comme ça :
On devine qu'il doit y avoir deux composantes (deux "bosses"). Il sera important de préciser à l'algorithme combien de composantes il y a, sans quoi le résultat sera n'importe quoi.
Ensuite il existe de nombreux packages à même de faire le travail. Voilà un exemple avec la librairie R "mixtools" :
library(mixtools) mixmodel = normalmixEM(data, k=2) # k=2 composantes mu = mixmodel$mu # moyennes ~ [2,6] sigma = mixmodel$sigma # écarts-types ~ [1,1.5] post = mixmodel$posterior # probabilités a posteriori lambda = mixmodel$lambda # proportions ~ [0.72,0.28] # Graphique par defaut plot(mixmodel, which=2) # Graphique perso (ci-dessous) plot(density(data), col='red', ylim=c(0,0.3), lwd=2) x = seq(min(data),max(data),length=1000) y1 = lambda[1]*dnorm(x,mu[1],sigma[1]) y2 = lambda[2]*dnorm(x,mu[2],sigma[2]) lines(x,y1,col='blue',lwd=2) lines(x,y2,col='green',lwd=2)
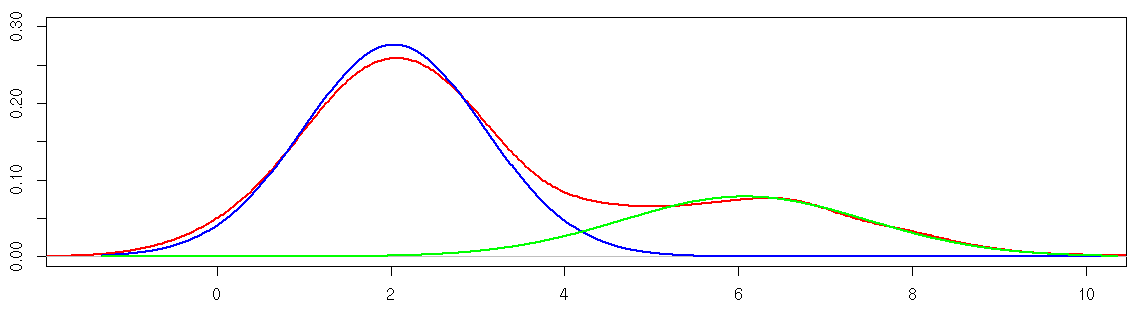
En rouge la densité jointe (non-paramétrique) ; en bleu/vert les courbes de densité des deux composantes normales, d'après les estimations de mixtools.
Et voilà, on a séparé les données en deux composantes normales. On peut ajouter à volonté au graphe la position des moyennes, les écarts-types, les points colorés selon leur appartenance à l'une ou l'autre composante, etc.
Alternativement, en utilisant la librairie "mclust" et en utilisant d'autres possibilités graphiques :
library(mclust) mixmodel = Mclust(data, G=2, model="V") # G=2 composantes, "V" pour variances non égales mu = mixmodel$par$mean # moyennes ~ [2,6] sigma = sqrt(mixmodel$par$variance$sigmasq) # écarts-types ~ [1,1.5] # Graphique mclust1Dplot(data, parameters=mixmodel$parameters, z=mixmodel$z, what="density", col='red', new=TRUE) hist(data, freq=FALSE, breaks=100, add=TRUE) abline(v=mu, col='blue') abline(v=c(mu+sigma,mu-sigma), col='blue', lty=2)

On a ajouté à l'histogramme des données la densité jointe (non-paramétrique, en rouge), la moyenne (bleu plein) et la variance (bleu trait-tillé) de chaque composante normale.
Généralisation
Notez que si dans notre exemple nous avons deux composantes normales à une dimension, on peut facilement généraliser à X composantes en N dimensions (comme dans l'exemple ci-dessous) mais aussi avec d'autres sortes de distributions de probabilité. Dans le cas de deux dimensions, la ligne de points de notre toute première figure ci-dessus devient un nuage de points dans un plan.
# On génère des données de test set.seed(1) pop1 = mvrnorm(n=1000, c(2,2), matrix(c(1,0,0,1),2) ) pop2 = mvrnorm(n=1000, c(7,7), matrix(c(1.5,0,0,9),2) ) pop3 = mvrnorm(n=1000, c(1,8), matrix(c(10,0,0,5),2) ) data = rbind(pop1,pop2,pop3) # La fonction mvnormalmixEM est l'équivalent multivarié. # On précise qu'on veut k=3 composantes. mvmixmodel = mvnormalmixEM(data, k=3) # Graphique par(mfrow=c(1,2)) plot(data,pch=4) plot(mvmixmodel, which=2, pch=4)

A gauche les données initiales ; on devine trois sous-groupes. A droite, la décomposition par mixtools, où on a coloré les points selon la composante à laquelle ils appartiennent le plus probablement.
Remarque : le calcul a tout de même pris une bonne dizaine de minutes sur mon vieux Mac.
Il existe dans à peu près tous les langages des librairies de ce genre. Un exemple notable est le tout prometteur langage Julia, encore en développement, qui possède une librairie "MixtureModels", par exemple :
using MixtureModels using Distributions obs = vcat( rand(Normal(2,1),1000), rand(Normal(6,1.5),400) ) r = fit_fmm(Normal, obs, 3, fmm_em()) r.mixture.components # liste des composantes normales r.mixture.pi # proportions r.Q # probabilités a posteriori
Parfois c'est plus compliqué : l'algorithme EM peut être implémenté dans sa forme générale (il a beaucoup d'autres usages), et c'est à vous de spécifier à quoi l'appliquer. Mais c'est un autre sujet qui mérite un livre à lui tout seul.
Merci à ook4mi, frvallee, Bu, ZaZo0o et Yoann M. pour leur relecture.
Toutes les figures sont de l'auteur de l'article.



